¶ OPERATORS
¶
plus

Addition (usually signified by the plus symbol +) is one of the four basic operations of arithmetic, the other three being subtraction, multiplication and division. The addition of two whole numbers results in the total amount or sum of those values combined.
For example, 3 + 2, spoken as "3 plus 2", meaning 3 and 2 is added together, totaling 5. Therefore, the sum of 3 and 2 is 5; that is, 3 + 2 = 5.
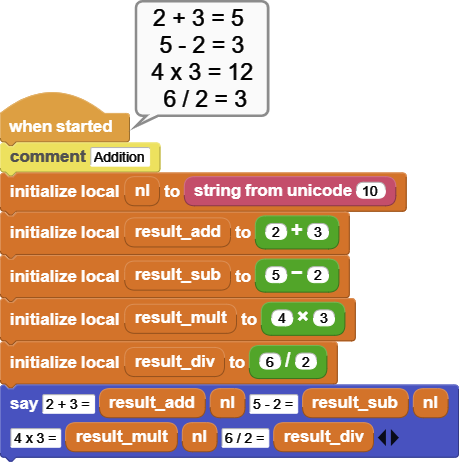
The examples for the four basic operations are all presented in a single sample script.
Add: 2 + 3 = 5
Sub: 5 - 2 = 3
Mul: 4 x 3 = 12
Div: 6 / 2 = 3
¶
minus

Subtraction (which is signified by the minus sign −) is one of the four arithmetic operations along with addition, multiplication and division. Subtraction is an operation that represents removal of objects from a collection.
For example, 5 − 2, spoken as "5 minus 2", meaning 5 with 2 taken away, resulting in a total of 3. Therefore, the difference of 5 and 2 is 3; that is, 5 − 2 = 3.
The examples for the four basic operations are all presented in a single sample script.
Add: 2 + 3 = 5
Sub: 5 - 2 = 3
Mul: 4 x 3 = 12
Div: 6 / 2 = 3

¶
multiply

Multiplication (often denoted by the cross symbol ×, or by an asterisk *) is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a product.
The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the multiplicand, as the quantity of the other one, the multiplier; both numbers can be referred to as factors.
For example, 4 multiplied by 3, often written as 3 × 4, and spoken as "3 times 4", can be calculated by adding 3 copies of 4 together:
3 × 4 = 4 + 4 + 4 = 12
Here, 3 (the multiplier) and 4 (the multiplicand) are the factors, and 12 is the product.
The examples for the four basic operations are all presented in a single sample script.
Add: 2 + 3 = 5
Sub: 5 - 2 = 3
Mul: 4 x 3 = 12
Div: 6 / 2 = 3

¶
divide

Division is one of the four basic operations of arithmetic. The other operations are addition, subtraction, and multiplication. What is being divided is called the dividend, which is divided by the divisor, and the result is called the quotient.
At an elementary level the division of two natural numbers is, among other possible interpretations, the process of calculating the number of times one number is contained within another. The division of whole numbers may be thought of as repeated subtraction, meaning how many times a number can be subtracted from another one.
For example, 6 divided by 2, often written as 6 / 2, and spoken as "6 divided by 2", can be calculated by subtracting 2 three times from 6:
6 / 2 = 3
6 - 2 = 4 (1x)
4 - 2 = 2 (2x)
2 - 2 = 0 (3x)
The examples for the four basic operations are all presented in a single sample script.
Add: 2 + 3 = 5
Sub: 5 - 2 = 3
Mul: 4 x 3 = 12
Div: 6 / 2 = 3

¶
modulus

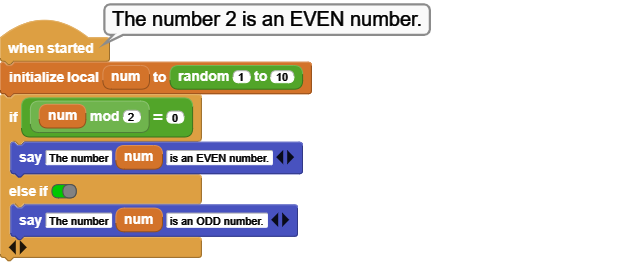
The modulus (or "modulo" or "mod") is the remainder after dividing one number by another. e.g.: 10 mod 3 equals 1. Because 10/3 = 3 with a remainder of 1.
The variable num is assigned a random number 1-10. The MOD operation is used to probe the odd/even status of the number. If the remainder of the operation num divided by 2 results in 0, the number is even, else it is odd.
¶ abs

Returns the magnitude of the given number (always >= 0).
¶ min

Returns the smaller of the values.
Using the black right traingle, additional fields can be added to the comparison.
¶ max

Returns the larger of the values.
Using the black right traingle, additional fields can be added to the comparison.
¶
random

Returns a different number between first and second values specified.
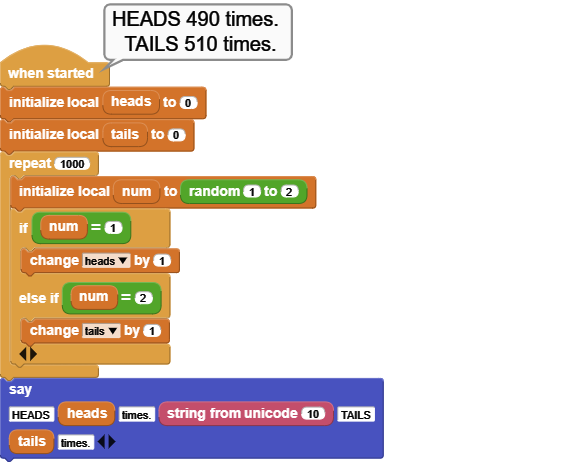
One of the common beginners' use of the RANDOM function is to program a HEADS or TAILS implementation.
Here, two variables heads and tails are created, as well as a variable num to store the result of the RANDOM function.
In a loop of 1000 repetitions, heads and tails counts are tallied. Arbitrarily, 1 is counted as heads and 2 is counted as tails. The results are displayed at the end.
¶ sum

Returns the sum of the argument values.
Right triangle can be clicked to provide more than one argument.
¶ less than

Returns true if the first value is smaller than the second one.
¶ less than or equal

Returns true if the first value is smaller than or equal to the second one.
¶ equal

Returns true if both values are equal.
¶ not equal

Returns true if the two values are not equal.
¶ greater than or equal

Returns true if the first value is greater than or equal to the second one.
¶ greater than

Returns true if the first value is greater than the second one.
¶
boolean true/false

Returns true or false depending on the position of the selector, or the binary evaluation of the expression used as input.
You will see this block inside of many other blocks, where it is used to control the flow of the executions and events.
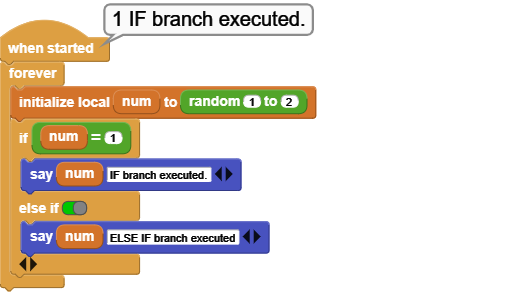
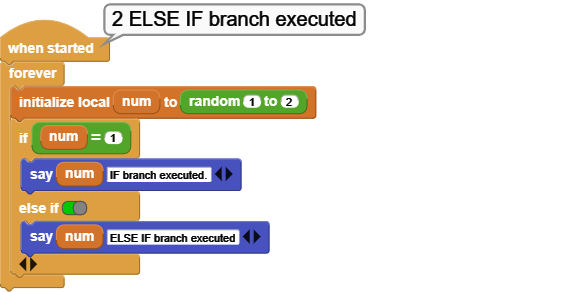
The IF block is a good example to demonstrate the true / false use of this block. The example code is executed two different ways:
First one is a FOREVER loop where the ELSE IF branch of the IF block is set to FALSE - meaning: do NOT evaluate this branch. Therefore, when run, only the first display message is shown. Even though the random block produces 2's, it does not get evaluated, because the else branch is turned off with the FALSE setting.
Also to note is the expression next to the IF. Originally, this position is the true / false block. It gets replaced by the expression num = 1. The binary evaluation of this expression is either true or false depending on what the generated number is. This demonstrates that expressions that evaluate to true or false can be used in place of this block.

In the second one, the FOREVER loop is removed, and the ELSE branch is set to TRUE - meaning: evaluate this branch, if the IF branch is not true. So, if num is not 1 (meaning it is 2), this branch will execute and second message will be shown.
Since the random block generates 1's and 2's, the corresponding message is displayed depending on the number generated.
 |
 |
|---|
¶
boolean not

Reverses the logical value associated with the expression on which it operates.
As shown, NOT will return FALSE if the slider is set to TRUE, and TRUE if the slider is set to FALSE.
It is also possible to substitute an expression that evaluates to a boolean true or false into the input slot. In that case, the block will evaluate the expression and depending on the result, return the opposite boolean value.
A variable called string is set to "MicroBlocks is great", and a variable called expression is set to "length of string = length of string".
The boolean evaluation of the expression is obviously TRUE.
When the boolean NOT is applied to the expression result, it is changed to the opposite: FALSE. All values are displayed.

¶
boolean and

Returns true only if either of its inputs are true and returns false otherwise.
It should be noted that since both conditions are required to be true for a true result, if a false is detected in the first condition, there is no need to evaluate the second one; false is returned immediately.
Two variables tuesday and raining are set to true.
Then we check to see if we need an umbrella by evaluating if it is Tuesday and it is raining. Both conditions have to be true for us to need an umbrella.
Play with settings and decidde yourself.

¶
boolean or

Returns true if either or both operands is true and returns false otherwise.
Similar to the boolean_AND but opposite of it, here only one of the two conditions have to be true for a true result. So if the first condition is true, there is no need to check the second one.
In this example we are randomly generating two numbers in the range of 1 - 5. Then we check to see if either one of the two numbers is equal to the number we are looking for.
OR block is used to verify the result of the comparison. All values are reported.

¶ toString

Returns the input expression converted to String.
¶
is type

Returns true if the input expession on the left side matches the data type menu selection made on the right side.
Data types are important when programming. While an environment like MicroBlocks makes it easy for the beginner users by taking care of any data type conversions, it is still possible to be fooled visually when comparing variables whose values look the same. See example provided.
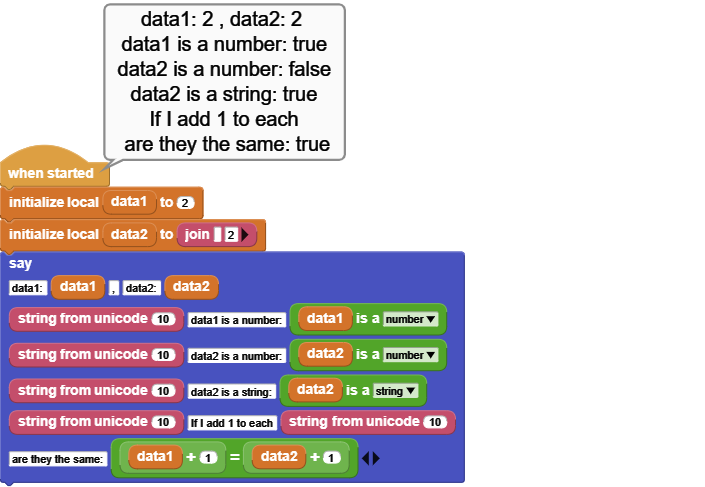
Two variables data1 and data2 are set to similar looking values:
data1 is set to number 2
data 2 is set to string "2".
IS TYPE block is used to verify the types of the variables. Even though they look the same, they are of DIFFERENT types.
Then we do arithmetic with both fields by adding 1 to each.
Since the data1 is already a number, no problems there.
data2 is a string, but has no visible alphabetic characters in front of the "2".
Therefore, MicroBlocks is able to convert it to number 2 for us, and do the addition.
At the end, when we compare the values of data1+1 to data2+1, we get a TRUE because both of expressions evauate to number 3.
Now try the same after placing any letter into the first input field of the join block for data2, and see what results you will get.
¶
convert

Returns the input expession on the left side converted to the data type menu selection made on the right side.
Data types are important when programming. While an environment like MicroBlocks makes it easy for the beginner users by taking care of any data type conversions, it is still possible to be fooled visually when comparing variables whose values look the same. This block will help you with conversion between any of the object types supported by MicroBlocks.
| TYPE | DESCRIPTION | VALUES | COMMENTS |
|---|---|---|---|
| Booleans | Represent the values true and false. | true: other than 0, false: 0 | |
| Integers | Store signed 31-bit two's-compliment values. | -1073741824 to 1073741823 | |
| Byte Arrays | Store unsigned 8-bit Integer values. | 0 - 255 | fixed size, cannot grow dynamically. |
| Strings | Strings are a sequence of characters used to store words or plain text. Characters may be a letter of some alphabet, a digit, a blank space, a punctuation mark, etc. Characters are stored as UTF-8 encoded Unicode code points. |
hex: U+0000 - U+10FFF or dec: 0 - 69631 |
First 128 UTF-8 code points correspond to the ASCII character set. |
| Lists | Store any of the objects listed above. |
As an example, we will use an integer number 123 and convert it to a boolean type.
Per the boolean description in the data type table above, all integer values greater than 0 convert to boolean True. And integer value 0 converts to boolean False.
Change the integer value in the example and see what results you get.

¶
Advanced
This section contains some blocks that represent bitwise operations.
The bitwise operators are similar to the logical operators (booleans), except that they work on binary representations of data.
Bitwise operators are used to change individual bits in an operand.
Both operands associated with the bitwise operator must be integers.
To make it easier to follow the details and examples presented below, a reference table detailing Byte Positional values in decimal and hex, have been provided.
Byte Positions and Values
Byte Position: 7 6 5 4 3 2 1 0 Decimal Value: 128 64 32 16 8 4 2 1 Hex 80 40 20 10 08 04 02 01
¶ Anatomy of a binary number:
A binary number is a number expressed in the base-2 numeral system or binary numeral system, which uses only two symbols: typically "0" (zero) and "1" (one).
A byte is an eight bit binary number. Each bit is either a 0 or a 1.
To determine the decimal value of a binary number of eight bits, refer to the Byte Position table and add all decimal values for columns where the binary number has a 1.
Example:
Binary Number: 0010 0110 Decimal Value: 38
Explanation:
| Byte Position: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Decimal Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Binary Number | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Total all the decimal values with a binary 1 in that column:
Decimal Values: 32 + 4 + 2 = 38
¶
ternary if

The condition expressed in the first position is evaluated. If TRUE, expression in second position is returned or if FALSE, the expression in the third position is returned.
While functionally very similar to the IF-THEN-ELSE construct, the fact that this block is a reporter, gives it extra usability. The value returned can be placed in other operations directly inline, without the cumbersome if-then-else block structure.
The condition expressed in the first slot has to evaluate to a true/false result.
Second and third slot values can be expressions that evaluate to any data type. In addition, these can also be function names or call statements referring to function names; providing ultimate flexibility and compactness in the code written.
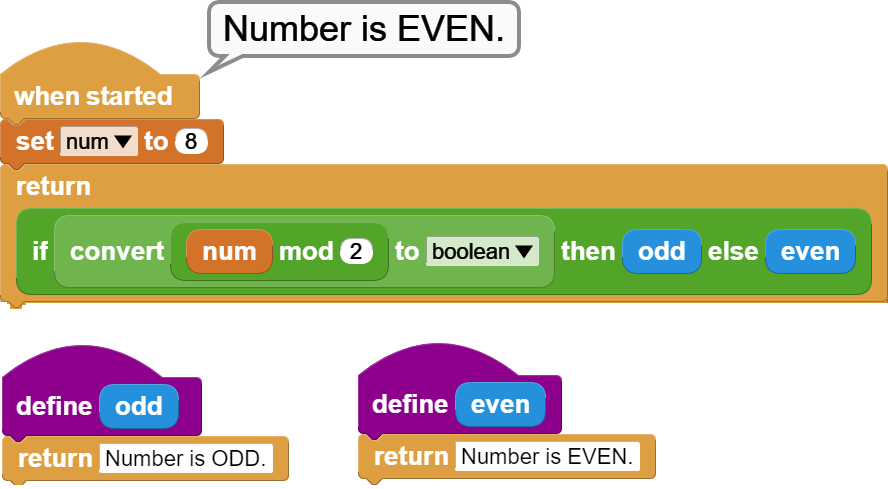
A simple example would be odd/even evaluation of a number.
The MOD operation returns the remainder of two numbers divided by each other.
If we use a division by 2, then if the result is 0, the number is even; and if the result is not 0, the number is odd.
To convert the division result into a true/false format, we use the convert operation with the boolean option.

A second version of the same example uses custom functions that return the evaluation results as "Number is ODD" or "Number is EVEN". These function names are used as second and third slot values.
¶
rescale

It takes a value expressed in the first input slot and scales it from the "from" range to the "to" range. The value in the first input slot has to be within the "from" range.
This is a very useful function that is often used to adjust the PWM values returned by the analog pins.
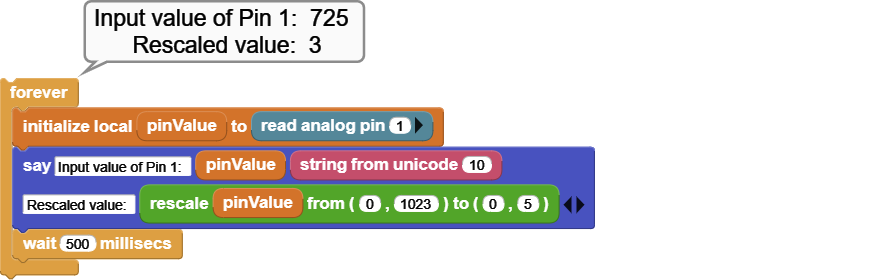
We have a potentiometer attached to pin 1 of the microcontroller. Manipulating the potentiometer generates values in the range of 0-1023. We will convert these values to the range of 0-5 for our application.
We read the analog pin 1 value and store it in a variable called pinValue. We then use the variable as in input into the rescale block's first parameter. The "from" range of the rescale block is set to the potentiometer range of 0-1023. The "to" range of the rescale block is adjusted to our desired range of 0-5.
¶
sqrt

Returns the square root value of the number input.

¶
arctan

The basic formula for the arctan is given by, arctan (Perpendicular/Base) = a, where a is the angle between the hypotenuse and the base of a right-angled triangle. We use this formula for arctan to find the value of angle a in terms of degrees or radians.
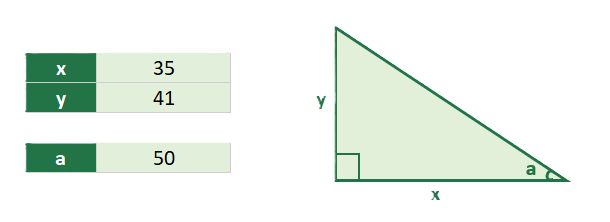

Due to the fact that MicroBlocks works with integer math, the result is provided in a multipled by 100 format. To get the actual angle value, divide by 100.

If you wish to preserve the fractional angle value, you can use the mod function.

¶
hex

Converts a hexadecimal string to a decimal number.
As a quick intro, hex numbers consist of 0 - 9 and A, B, C, D, E, F.
Thus, hex(3F) evalutes to 63 in decimal.
Note that HEX block inputs have to be of type STRING, since part of the hex numbers consist of letters A -F.
hex to decimal conversion is a very common operation. Each hexadecimal digit represents exactly four bits, so one byte is represented by two digits. That simple mapping between digits and bytes makes hexadecimal useful when working with certain kinds of data. For example, RGB color codes.
Dec - Hex - Bin Number Conversion
Decimal Hex Binary Decimal Hex Binary 0 00 0000 8 08 1000 1 01 0001 9 09 1001 2 02 0010 10 0A 1010 3 03 0011 11 0B 1011 4 04 0100 12 0C 1100 5 05 0101 13 0D 1101 6 06 0110 14 0E 1110 7 07 0111 15 0F 1111
 |
|---|
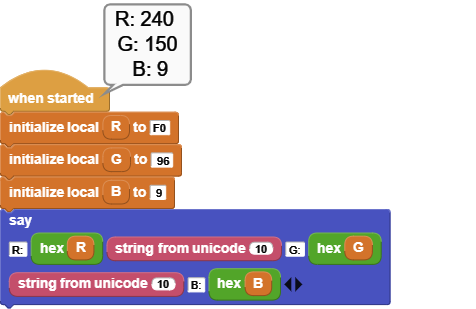
Chrome browser's "Color For Developer's" extension enables one to pick a color from a suite of color palettes used on the web. The color is displayed in RGB format as three hex numbers.
If we want to set the CLUE rgbLED color using the Neopixel Library blocks, we need to convert the RGB values into decimal equivalents.
Example program accepts three hex numbers and displays their decimal equivalents. It then sets the NeoPixel RGB values accordingly.
 |
 |
|---|
¶
bitwise and

The AND operator compares two bits and generates a result of 1 if both bits are 1; otherwise, it returns 0.

Explanation:
| Byte Position: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Decimal Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 13 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Result = 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
- Bitwise AND compares all the bit positions of both numbers and reports the ones where both are set to 1.
- Between #13 and #7, the positions where both numbers have a 1 are positions 2 and 0.
- The decimal value of position 2 is 4, and of position 0 is 1.
- Therefore the operation reports 4 + 1 = 5.
¶
bitwise or

The OR operator compares two bits and returns 1 if either or both of the bits are 1 and it gives 0 if both bits are 0.

Explanation:
| Byte Position: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Decimal Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 115 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Result = 123 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
- Bitwise OR compares all the bit positions of both numbers and reports the ones where either are set to 1.
- Between #115 and #9, the position where either numbers have a 1 are positions 6,5,4,3,1, and 0.
- The decimal value of position 2 is 4, and of position 0 is 1.
- Therefore the operation reports 64 + 32 + 16 + 8 + 2 + 1 = 123.
¶
bitwise xor

The EXCLUSIVE-OR operator compares two bits and generates a result of 1 if the bits are complementary (bit is set in one operand but not both); otherwise, it returns 0.
Another way to think of the XOR operation is that it will reverse the bit positions where the second operand has a 1. All others will be copied as the same.

Explanation:
| Byte Position: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Decimal Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 11 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 12 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| Result = 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
- Bitwise XOR compares all the bit positions of the first operand and reports the opposite of where the second operand has a 1.
- #12 has a 1 in positions 3 and 2. Bits in the same positions of #11 ( 10 ) will be reversed, all other bits of #11 will be copied as they are. For position 3 and 2 reversed, we get 01.
- We end up with 0000 0111 for the result. Positions 2, 1, and 0 are 1.
- The decimal value of position 2 is 4, position 1 is 2, and position 0 is 1.
- Therefore the operation reports 4 + 2 + 1 = 7.
¶
bitwise not

The NOT (or COMPLEMENT) operator is used to invert (BIT FLIP) all of the bits of the operand.
When the highest position bit of a number becomes 1, that number is considered a negative number.
Actual computer representation of an signed integer in MicroBlocks is 31 bits long. The high order bit #31 is a sign bit. This allows numbers in the range of -1073741824 to 1073741823.
When the sign bit is 0 the number is positive; and when it is 1, the number is negative.
NOT operation reverses all bits and turns positive numbers into negative ones and vice versa.

Explanation:
NOT operation reverses all bits and turns positive numbers into negative ones.
Decimal 3 ( Binary: 0011 ) becomes decimal -4 ( Binary: 1100 ).
NOTE: In the 4-bit example used here, the high order bit (bit-3) is the sign bit.
¶
bitwise left shift

The left operands value is moved left by the number of bits specified by the right operand.
The bits are moved to the left, the far left bit is discarded, and the rightmost bit is assigned a value of 0.
For every bit position moved to the left, this operation is the binary equivalent of multiplying by 2.
REMEMBER
For signed positive numbers that naturally have a 0 bit in the most significant position of their binary representation, this operation will eventually turn that into a 1 bit, thus changing the number to a negative one.

Decimal number 7 is Left shifted 1 bit position.
Bit positions of the result are: positions 3, 2, and 1; with corresponding values of 8, 4, 2.
Therefore the operation reports: 8 + 4 + 2 = 14.
Explanation:
| Byte Position: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Decimal Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 14 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
¶
bitwise right shift

The left operands value is moved right by the number of bits specified by the right operand.
The bits are moved to the right, the far right bit is discarded, and the leftmost bit is assigned a copy of the sign bit. This is called an arithmetic shift.
For every bit position moved to the right, this operation is the binary equivalent of dividing by 2.
REMEMBER
For signed negative numbers that naturally have a 1 bit in the most significant position of their binary representation, this operation will maintain the sign bit and successively produce negative numbers.

Decimal number 7 is Left shifted 1 bit position.
Bit positions of the result are: positions 4, 3, 1, and 0; with corresponding values of 16, 8, 2, and 1.
Therefore the operation reports: 16 + 8 + 2 + 1 = 27.
Explanation:
| Byte Position: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Decimal Value: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 54 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 27 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |


































